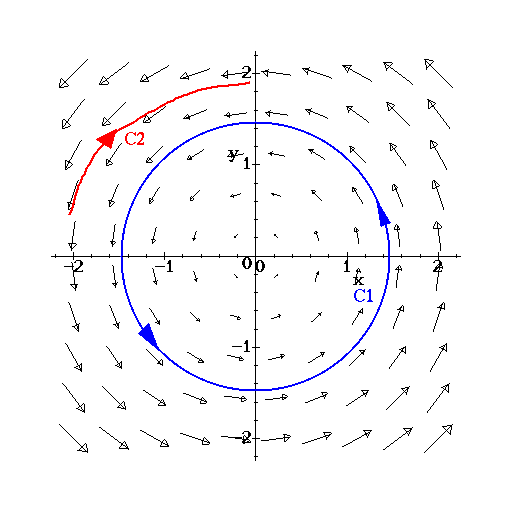
Showing that capital f exists is the way you find out if the vector field is conservative. F = m i n j is defined in a connected and. The work done to carry a test charge (q) from point a to another point b in the field due to. Thus, we have way to test whether some vector field a()r is conservative: Sep 14, 2018 at 22:30.
The reason such fields are called conservative is that they model forces of physical systems in which energy is conserved. Contact us +44 (0) 1603 279 593 ; × e = − ≠ 0. Web since we know that this is a conservative field, we can apply theorem 1, which shows that regardless of the curve c, the work done by f will be as follows:
The following conditions are equivalent for a conservative vector field on a particular domain : Showing that capital f exists is the way you find out if the vector field is conservative. Web a conservative field f is a gradient of some scalar, do that f = ∇ u.
Ds = 0 ∮ c f →. In physics, because of the connection of the scalar u to potential energy, the conservative field is typically taken as f = − ∇ u. At every point in the domain. The scalar u is called the scalar potential for f. The integral is independent of the path that c c takes going from its starting point to its ending point.
If and only if m y n x. Web in vector calculus, a conservative vector field is a vector field that is the gradient of some function. There exists a scalar potential function such that , where is the gradient.
∇ × = − ≠ 0.
If the result equals zero—the vector field is conservative. There exists a scalar potential function such that , where is the gradient. At every point in the domain. Work and energy of a charged particle.
If There Is No Capital F That Exists For That Vector Field, Then Your Vector Field Is Not.
Consider an electric field created due to a charge q. First we check that f is conservative. My understanding of the conservative field is that it is any vector field that satisfies any of these three equivalent conditions: Examples are gravity, and static electric and magnetic fields.
For Any Closed Path C C In The Domain, F =∇ Φ F → = ∇ → Φ.
Explain how to find a potential function for a conservative vector field. A man of deep christian faith, his long career was devoted to eradicating poverty and improving the lives of the poor. (41.8.1) (41.8.1) ∮ any loop g → ⋅ d l → = 0. We can then say that, ∇f = ∂f ∂x →i + ∂f ∂y →j = p →i +q→j = →f ∇ f = ∂ f ∂ x i → + ∂ f ∂ y j → = p i → + q j → = f →.
Contact Us +44 (0) 1603 279 593 ;
For some scalar field ϕ ϕ defined over the domain, and. The work done to carry a test charge (q) from point a to another point b in the field due to. Or by setting components equal we have, In physics, because of the connection of the scalar u to potential energy, the conservative field is typically taken as f = − ∇ u.
× e = − ≠ 0. We study conservative vector fields in more detail later in this chapter. Is the electric field always conservative? Work done by the electric field. Over closed loops are always 0.